Blooming design

At Brew, we work with an infinite amount of marketing activities, such as blogs and webinars. To ensure the most effective workflows, the initial validation we always make is to check if this activity is already known to the Brew platform. This optimizes the process and saves significant time before we start running validations and data extractions on the activities we encounter. One of our ways to do this validation is by checking the activity’s URL.

Checking whether this URL already exists can be done by scanning the blog posts table, which has an O(N) complexity. This means that this search can become very heavy the more blog posts we have (just think of how many blog posts are published only on this platform).

Of course this search can be improved if we index the URL column, which will improve the search time from O(N) complexity to O(logN) complexity (shout out to B-tree indexes). But, even with this improvement, the search time can be quite long and it will get longer the more blog posts we get. Another way to optimize this search is by using a hash table for all values, but the cost of this solution is space complexity.

So how can we optimize this search with a balanced time and search complexity? This is where the Bloom filter comes in.

Probability vs Efficiency

A Bloom filter is a space-efficient probabilistic data-structure that is used to test whether a certain element is a member of a set. In simpler words, a Bloom filter allows us to check whether an element probably exists in a set, with an O(1) complexity. A Bloom filter is probabilistic which means we might get a false positive response. In our example, a false positive means that we searched for a URL using the Bloom filter and it returned that the URL exists in the database even though it doesn’t exist. As mentioned before, we will process only URLs that don’t exist already, so when we receive a false positive result, we actually lose some data (there is a solution for that, which will be discussed later).

But, we are guaranteed that the Bloom filter will not return a false negative, so we can be sure that we are not processing data that has already been processed.

Bloom in action

An empty Bloom filter is a bit array of m size, all set to 0. We need a k number of hash functions to calculate hashes for each input. When we receive a new input, we use the hash function on it. Each hash function’s result will be a number between 0 and m, which will represent an index in the bit array. After running the hash functions on an input, we will turn on the bits in the received indices.

Let’s assume that we are using a bit array of length 20 and 3 hash functions — h1, h2, h3. Now, we are adding the URL “http://cat.com” to our database. First, we run the hash functions on this address:

Now the bit-array will look like this:

Now we want to add a new URL address — “http://dog.com”. We run the hash functions on the new input:

Before adding this new value to our database, we want to be sure that it doesn’t exist. This is done by checking the bits in the indices that we received from the hash functions. If all bits are already on, we can say that the value “http://dog.com” probably exists. If not all bits are on, we can safely process this URL and add it to our database, and of course update the bit array accordingly.

Now our bit-array will look like this:

What happens if we try to add the URL “http://cat.com” again? We first run the hash functions and receive the results: 2, 5, 10. We check the indexes, and since they are all on, we can say that this address probably exists.

Why do we keep saying “probably exists”? Let’s take a look at another example. Assume we want to add the URL “http://mouse.com”. We run the hash functions on this input and receive the results:

Now we check the bit array and see that all bits are on. This means that the Bloom filter will return the answer “URL already exists” even though this URL doesn’t actually exist in our database, since the bits 3 and 13 were turned on by the value “http://dog.com” and the bit 2 was turned on by the value “http://cat.com”, but none of them was turned on by the value “http://mouse.com”.

False positives and the potential impacts

When using the Bloom filter we will always have a probability of getting a false positive, but we can control this probability by controlling the size of the bit array and the number of hash functions we use. A larger bit array and a larger number of hash functions means less false positives, but it also means less space efficiency and more latency. So, we will have to decide on the acceptable false positive rate and calculate the number of hash functions and the array size according to it.

I won’t get into this in this post, but there is a formula that allows us to calculate the dependency between the false positives probability, the number of elements in the set, the number of hash functions that we use and the length of the bit array.

Another important thing to note about Bloom filter is that it doesn’t support deletes. As we can see in our examples, multiple words can turn the same bit, so in order to remove a word we would have to check whether all bits can be turned off, which can be very inefficient.

Test before you scan

The example above showed how we can use the Bloom filter to check quickly whether an item is new and can be added to our database. In the example above we never actually check the database, we rely on the Bloom filter’s response in order to tell whether an item is new. But, this comes at a cost of some data loss, since we are not processing the false positive results. We can mitigate this data loss by searching the database when we get a positive result from the Bloom filter and validating whether this value actually exists. If we choose this solution, we solve the data loss issue but lose some of the optimization. Still, using Bloom filter instead of always querying the database to check whether this URL already exists, improves the runtime complexity. It reduces the number of times we need to access the database, and if most of the times we encounter new URLs and the Bloom filter’s false positive rate is low, we rarely access the database for this validation.

From false to true positives — Bloom filter complement¹

But what happens if I don’t want to get a false positive at all? Let’s assume that we have an allowed list of IPs that can connect to our server. Every time the server gets a request, we want to check quickly whether this IP is in the allowed list. In this case, we wouldn’t like to use the Bloom filter, because we might get a false positive, which means we might allow the wrong IP to connect to our server. We can check the database to validate positive results from the Bloom filter, but this will cause the validation to take a longer time and we want to avoid it, since we want to return the response as quickly as possible. This is a classic case in which we can use the Bloom filter complement.

A Bloom filter complement is a solution that is based on the Bloom filter and can be used when we are working with a known set and a known finite complement set. A list of IPs is a good example for a known set, because we can calculate all available IPs in the world. It doesn’t matter that it is a very large number, it is a closed set that can be calculated which makes it eligible for Bloom filter complement. In this case, our set will be the allowed list of IPs and the complement set will be all existing IPs in the world that are not in the allowed list of IPs. Another prerequisite of the Bloom filter complement is that the set and the complement set can’t be changed often. Let’s assume that a list of allowed IPs doesn’t change quite often.

So how does this work?

The algorithm uses two Bloom filters — one for the allowed list of IPs and one for the complement set. Since these two sets have a different size, we will use a different size for the Bloom filter and a different number of hash functions.

When we check an IP, we first check the allowed IPs Bloom filter. If the answer is negative, we can be sure that this IP is not allowed. If we get a positive response, we check the second Bloom filter. If the second response is negative, we can be sure that this IP is allowed, because it is definitely not in the “not-allowed” list. If we receive a positive response from both filters, this necessarily means that one of them is false positive, in this case, we will have to search the database for the definite answer. So this solution doesn’t completely remove the use of the database, but it does reduce it significantly, since we will only access it when we get a positive result from both filters.

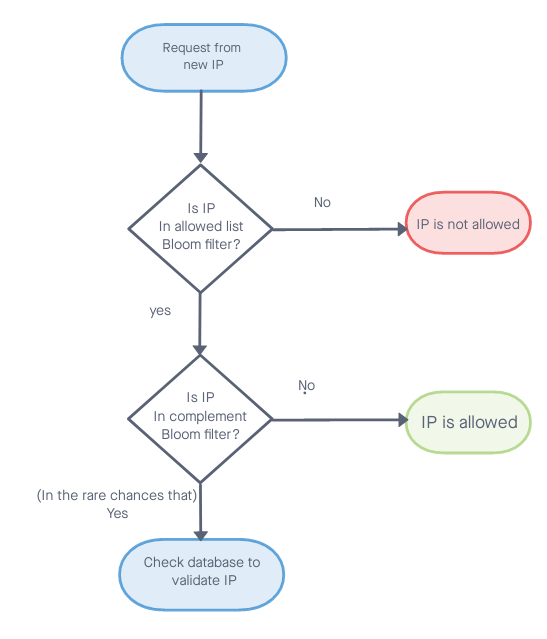
What happens if an IP is added or removed from the allowed list? In this case, we will have to recalculate both Bloom filters. This is why we will use this data structure only when there aren’t too many changes to the sets.

Bloom to optimize

Bloom filter is a common data structure that can be used for optimization of searches. These data structures can be used in databases, for example PostgreSQL, which supports Bloom filter indexes, and Redis with its RedisBloom module. Of course, we will choose to use this structure only when we can afford getting a false positive result. In cases where we can’t allow false positives, a Bloom filter is probably not the suitable solution.

The Bloom filter complement is an interesting solution that can be suitable for specific cases, but the uses cases for this data structure are not very common.

[1]: H. Lim, J. Lee and C. Yim, “Complement Bloom Filter for Identifying True Positiveness of a Bloom Filter,” in IEEE Communications Letters, vol. 19, no. 11, pp. 1905–1908, Nov. 2015, doi: 10.1109/LCOMM.2015.2478462